现在的这一节知识,是在学习了比例的知识之后才学习的,比例是两个数或两个式子作比较,而比例尺是拿实际的距离跟图上的尺寸作比较,这听上去很抽象,似乎不好理解,其实对于我们来说很熟悉,并不陌生,只是之前我们见它的时候,没叫它“比例尺”罢了,看下图。
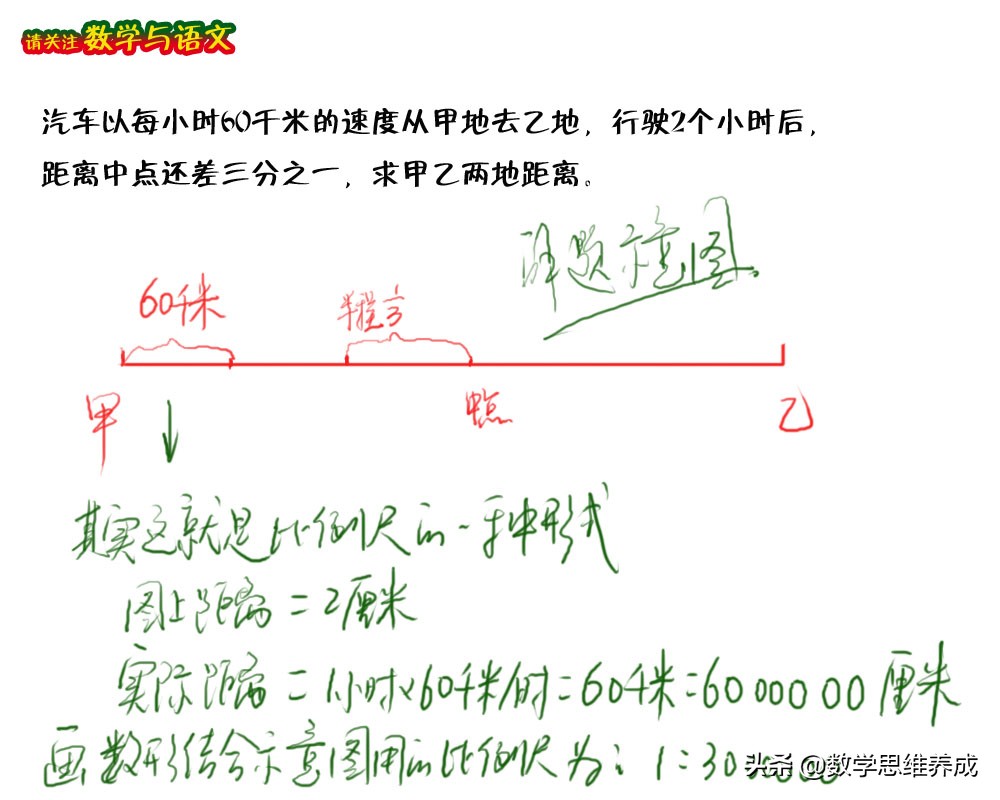
再比方说,蜗牛5分钟爬了多少路程,你可以很快画在纸上;如果让你把一个人5分钟跑步的路程画在纸上,可以吗?汽车呢?火箭呢?不可能了吧!如果非要在纸上表示它们跑过的路程怎么办?这时候就要用到可以缩小实际尺寸的比例尺了。
现在的晚会或演唱会,为什么要放个巨型的、好几个人高的LED屏幕呀?因为远处的观众看不清舞台上的人,通过这个巨型屏幕就可以看得很清楚。把人脸看成实际的尺寸,屏幕上的脸看成图上的尺寸,这在数学上是什么呀?不就是用到放大实际尺寸的比例尺吗!

但,不管是放大还是缩小,比例尺的概念不变,它表示的是图上线段的长度与实际的距离长度之比。我们可以写成这样来看(由公式推导的几个变形请看图片):
①比例尺 = 图上距离 :实际距离(比例形式)
②比例尺 = 图上距离 ÷ 实际距离(除法算式)
③比例尺 = 图上距离 / 实际距离(分数形式)
由这三个式子,记住“图上距离”是比例前项、被除数、分子;“实际距离”是比例后项、除数、分母,当看到如1:3000、1:500这样的,前面一项是“1”的比例尺,就知道是缩小的比例尺;当看到如30:1、500:1这样的,后面一项是“1”的比例尺,就知道是放大的比例尺。这是要说的第一个问题:如何区分比例尺是缩还是放。

从这里也可以看到,比例尺充分验证了古人的一句话——“失之毫厘谬以千里”。在这里说句题外话,在我国古代诗词里,是含有很多的数学知识的,“横看成岭侧成峰,远近高低各不同”,“两个黄鹂鸣翠柳,一行白鹭上青天”,“大漠孤烟直,长河落日圆”……学习数学主要是可以让我们的思维变得更严谨,做事更加细心,当然,顺带着背背古诗词,也可以提高一下我们的文学修养,文、数双修噢!

下面说第二个问题:比例尺为什么没有单位?这个可以看上面列出的式子②:
比例尺 = 图上距离 ÷ 实际距离,
很显然,“图上距离” 、“实际距离”都是有单位的,但是,它们这么一除就互相约掉了,看一下这张图,这样好理解吗?同时,这里还有一个非常重要的注意事项,在计算的时候,一定要把“图上距离” 、“实际距离”的单位换算成一样的,否则是没办法约掉的。

在实际绘制地图或图纸,或者我们平时作图的时候,一幅图里只能使用一个比例尺,如果长和宽使用不同的比例尺,就会发生变形或失真,“成比例缩放”就是要求的长宽按照同样的比例缩小或放大。上面说的大屏幕就是成比例缩放,想象一下,如果只是横向放大或竖向放大的话,那胖子们可高兴了,都苗条的不得了,本来就瘦的人可看不得了,真成竹竿了!

